Het deeltje in ruimte

Ik heb lang moeten nadenken over een goede beschrijving van een deeltje in ruimte, ik had al wat pogingen gedaan, maar die vond ik bij nader inzien onvoldoende overtuigend. In het onderstaande doe ik wederom een poging.
Voorafgaande aan een beschrijving van een deeltje in ruimte moet ik, misschien ten overvloede, herhalen dat het voor de meeste mensen heel moeilijk is om zich voor te stellen dat de begrippen tijd en afstand niet in de werkelijkheid bestaan, dat ze slechts ideeën betreffen en alleen als hulpmiddel kunnen worden ingezet. Het is echter noodzakelijk dat men zich ervan bewust is dat voor een beschouwing van de werkelijkheid de begrippen afstand en tijd niet van toepassing zijn. Meten van tijd en afstand zijn menselijke handelingen en niet een fysiek onderdeel van de natuur net zo min als de meetresultaten. Zelfs dat laatste is voor wetenschappers heel moeilijk te bevatten, getuige het in de theorie van de kwantummechanica in de werkelijkheid laten bestaan van een Plancklengte die, net als de meter, toch gewoon een maateenheid is. Ik zal nog (noodgedwongen) regelmatig het bovenstaande moeten aanhalen om te voorkomen dat de lezer afdwaalt.

de omvang van een deeltje

Rekening houdend met het voorgaande kan ik beginnen met het beschouwen van het deeltje, het kleinste ondeelbare stukje ‘materie’ dat in de werkelijkheid bestaat.
Een deeltje wordt ook wel proton of waterstofkern genoemd. Elk deeltje bestaat in de werkelijkheid, want deeltjes worden bijvoorbeeld gebruikt voor experimenten in deeltjesversnellers en dat doen ze niet met denkbeeldige, theoretische deeltjes. Door het onomstotelijk in de werkelijkheid bestaan van deeltjes is elk deeltje een entiteit en er zijn er heel veel van.
Een deeltje bevindt zich in ruimte en daarbij geldt een belangrijke stelregel:
een deeltje=niet-ruimte; en daaruit volgt: ruimte=niet-deeltje.
Hoe eenvoudig deze stelregel ook lijkt, deze verhouding tussen ruimte en deeltjes is van cruciaal belang bij verdere analyses en beschouwingen.
Als ik een deeltje beschouw, dan kan dat alleen met mijn verstand; het deeltje zelf is fysiek niet waar te nemen, alleen de effecten op de omgeving ervan kunnen met een speciale transmissie-elektronenmicroscoop (TEM) en Scanning Tunneling Microscopen (STM) worden waargenomen (bron: Google Gemini).

Deeltjes zijn de bouwstenen van alle in de werkelijkheid bestaande objecten, zoals atomen, moleculen, voorwerpen, gassen etc.
Er wordt in de natuurwetenschappen gesteld dat een deeltje een diameter heeft van ‘ongeveer’ 0,1 nanometer (10^-10 meter) en daarmee kom ik meteen op de grootste denkfout in de natuurwetenschappen; ik zal dat proberen uit leggen.
Deeltjes zijn de enige objecten die in direct contact met ruimte staan, want een deeltje bevindt zich in ruimte; alle andere fysieke, in de werkelijkheid bestaande objecten zijn uit deeltjes (de bouwstenen) samengesteld, alleen deeltjes hebben echter direct contact met ruimte. Het raakvlak tussen ruimte en deeltje is de grens tussen de wereld van ruimte en de wereld van de ‘substantie’ van het deeltje. Ruimte en deeltje zijn twee van elkaar gescheiden werelden; alle veranderingen die in het universum plaatsvinden vinden plaats in ruimte en aangezien een deeltje niet-ruimte is kan een verandering niet in een deeltje zelf plaatsvinden.
Een deeltje in de werkelijkheid kan geen eigenschappen bezitten die tot de wereld van de menselijke ideeën behoren, zoals bijvoorbeeld in het synthetische oordeel: een deeltje heeft een diameter van ‘ongeveer’ 0,1 nanometer (10^-10 meter). Ik heb in het begin van deze essay gememoreerd dat het begrip afstand, dus ook het begrip diameter niet in de werkelijkheid bestaat; een deeltje kan daarom geen afmeting, geen omvang, geen doorsnede ‘bezitten’ en daarom heeft een deeltje een omvang van nul; een deeltje ‘is’ of ‘bezit’ geen afmeting, want afmeting is iets dat wij denken in een synthetisch oordeel over een deeltje in ruimte.
De oorzaak van de denkfout (dat een deeltje wel een afmeting heeft) ligt in ons menselijk voorstellingsvermogen; wij kunnen ons niet voorstellen dat een deeltje er wel is en tegelijk een omvang van nul heeft, daarom kennen we er gemakshalve een afmeting aan toe, zo kunnen we het tenminste met ons verstand ‘zien’. Door deze tekortkoming te beseffen en door te accepteren dat een deeltje geen afmeting kan hebben ligt ineens een nieuwe wereld voor ons open; een ontdekkingswereld die de basis vormt voor het verklaren van bijvoorbeeld zwaartekracht en bijvoorbeeld van adhesie en cohesie (aantrekkingskracht) tussen atomen en moleculen.
Het is gebleken dat het bedrijven van wetenschap een zuiver menselijke bezigheid is waarbij op een menselijke manier wordt beschouwd en dat menselijke vertaalt zich weer in de dwalingen, getuige het voor mij onvergetelijke optreden van Robbert Dijkgraaf in DWDD op 8 september 2011 waarin hij de mogelijkheden van tijdreizen aanhaalde terwijl we toch zeker weten dat de kalender niet in de werkelijkheid bestaat. In ieder geval: ondanks ons menselijk dwalen heeft een deeltje echt geen omvang.

wat doet een deeltje met ruimte

Ruimte betreft alleen de weg waarlangs veranderingen plaatsvinden. Als er een verandering plaatsvindt, dan is dat alleen in ruimte mogelijk, niet in een deeltje op zich, want een deeltje is immers niet-ruimte.
Als er zoiets als afstand zou moeten worden gemeten, dan is dat alleen in ruimte mogelijk, niet in een deeltje. Een deeltje ‘bestaat’ echter en omdat het bestaat moet het, ondanks het feit dat het voor ons geen afmeting heeft, zoiets als substantie hebben. Een deeltje heeft daarom een eigen wereld die niet-ruimte is.
Ruimte heeft ook een eigen wereld die niet-deeltje is en dat is de wereld waarin wij onze gewaarwordingen hebben, dus onze wereld.
We kunnen beide werelden wel beschouwen, maar nooit tegelijkertijd. We beschouwen met ons verstand de wereld van het deeltje of de wereld van ruimte.
Een deeltje bevindt zich in ruimte en heeft door zijn aanwezigheid in ruimte invloed op de weg, het doet er iets mee. Ik kan dat het duidelijkst laten zien in de volgende afbeelding:

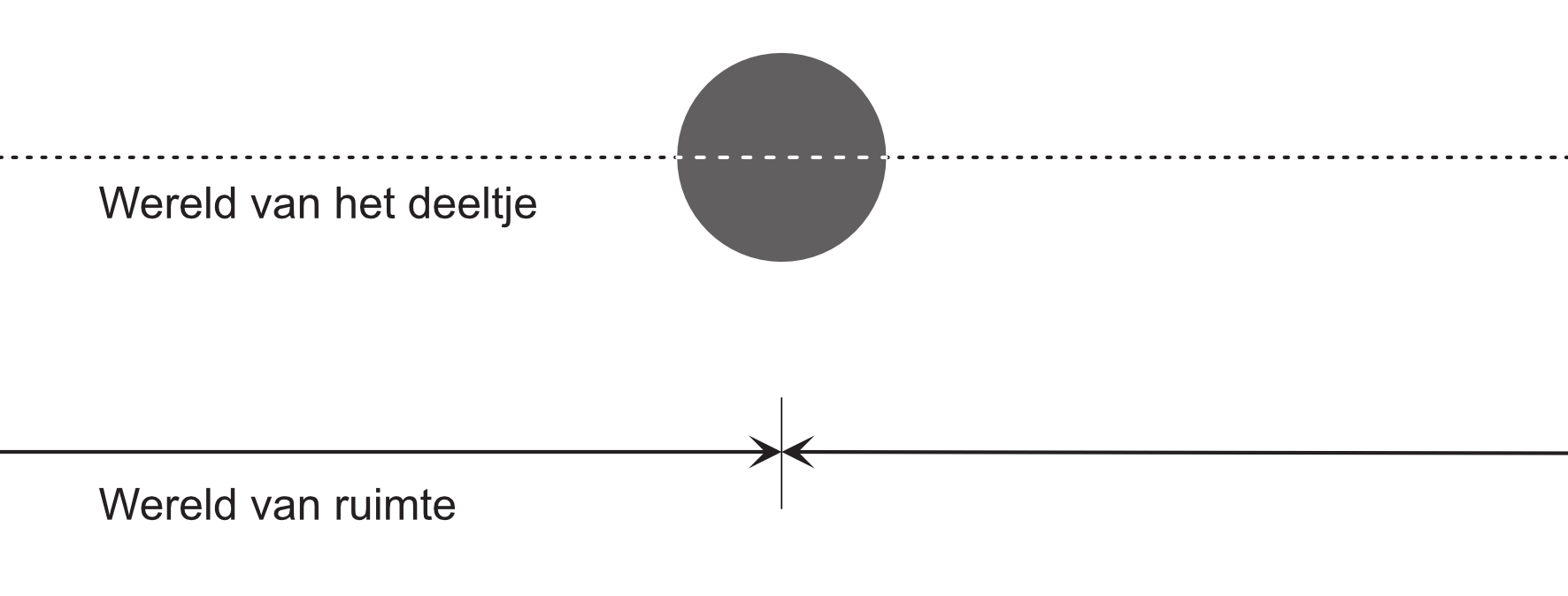
In de wereld van het deeltje zien we een deeltje, maar eigenlijk gaat het hier om het raakvlak tussen deeltje en ruimte, dus waar ruimte eindigt en deeltje begint. Wat achter dat raakvlak in een deeltje is zullen we nooit kunnen weten. Ik noem het dus wel de wereld van het deeltje, maar ik stel me eigenlijk alleen het raakvlak voor. De stippellijn stelt een weg voor die zich oorspronkelijk op de plaats van het deeltje zou moeten bevinden. Deze stippellijn die een weg in ruimte voorstelt reikt oneindig ver. Het witte stukje stippellijn in het deeltje is het stukje weg dat door de aanwezigheid van het deeltje aan ruimte ontbreekt, want een deeltje is niet-ruimte en dus niet-weg.
In het onderste gedeelte van de afbeelding, in de wereld van ruimte, is de weg ingekort door het ontbreken van het stukje weg dat door het deeltje is weggenomen. De weg is uitgerekt naar de plaats waar het deeltje zich in de wereld van ruimte bevindt. Dat uitrekken doet iets met de weg, de weg is veranderd. Ik zal dat duidelijk maken met de volgende afbeelding:

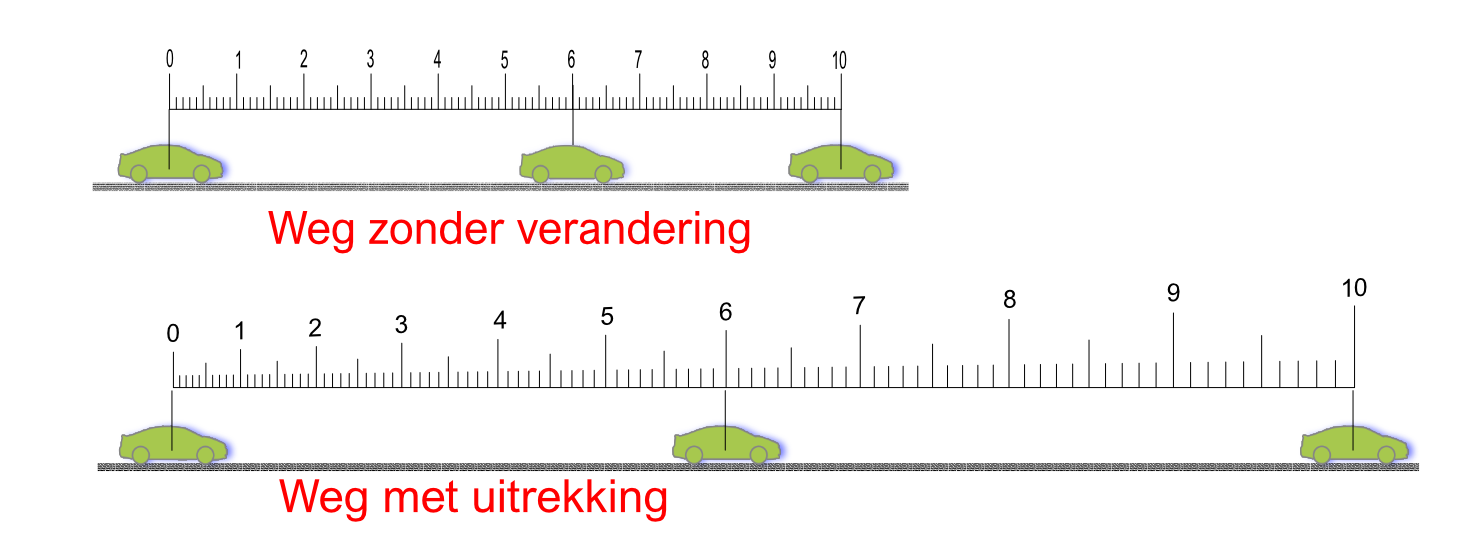
Ik laat in deze afbeelding twee situaties zien, een weg zonder verandering en een lineair toenemend uitgerekte weg waarbij ik de weg heb verdeeld in tien gemarkeerde stukjes om het verloop weer te geven.
De autootjes gaan bij markering 0 tegelijk van start en hebben dezelfde voortgang over de weg. Beide autootjes zijn tegelijk bij markering 10; het leek echter of het onderste autootje harder ging, maar omdat het dezelfde weg van tien markeringen aflegde gingen ze in werkelijkheid even hard. In de wereld van ruimte zorgt een deeltje voor een uitrekking van alle wegen die naar het deeltje leiden.
De uitrekking naar het deeltje wordt sferisch verdeeld over de hele ruimte. Deze sferische verdeling verloopt volgens de zogenaamde omgekeerde kwadratenwet.
De omgekeerde kwadratenwet stelt dat de intensiteit van een fysische grootheid (zoals licht, geluid, zwaartekracht, straling) omgekeerd evenredig is met het kwadraat van de afstand tot de bron. Dit betekent dat als je de afstand verdubbelt, de intensiteit vier keer zo klein wordt, en bij verdrievoudiging negen keer zo klein, omdat de invloed over een groter bolvormig oppervlak wordt verdeeld. De afname van de uitrekking vanaf het deeltje is dus niet lineair zoals in de bovenstaande afbeelding met de autootjes, maar volgt het kwadraat van de afstand (1/afstand²). Let wel: ik gebruik hier afstand als hulpmiddel om de beschouwing te begrijpen.
Hoe dichter je in ruimte bij het deeltje komt, des te sterker wordt de uitrekking. Op het raakvlak tussen ruimte en deeltje is de uitrekking in ruimte bijna oneindig groot.

de A- en B-richting

Uitrekking, zoals ik hierboven heb beschreven, staat niet op zich en dat kan ik het beste uitleggen met de volgende afbeelding:

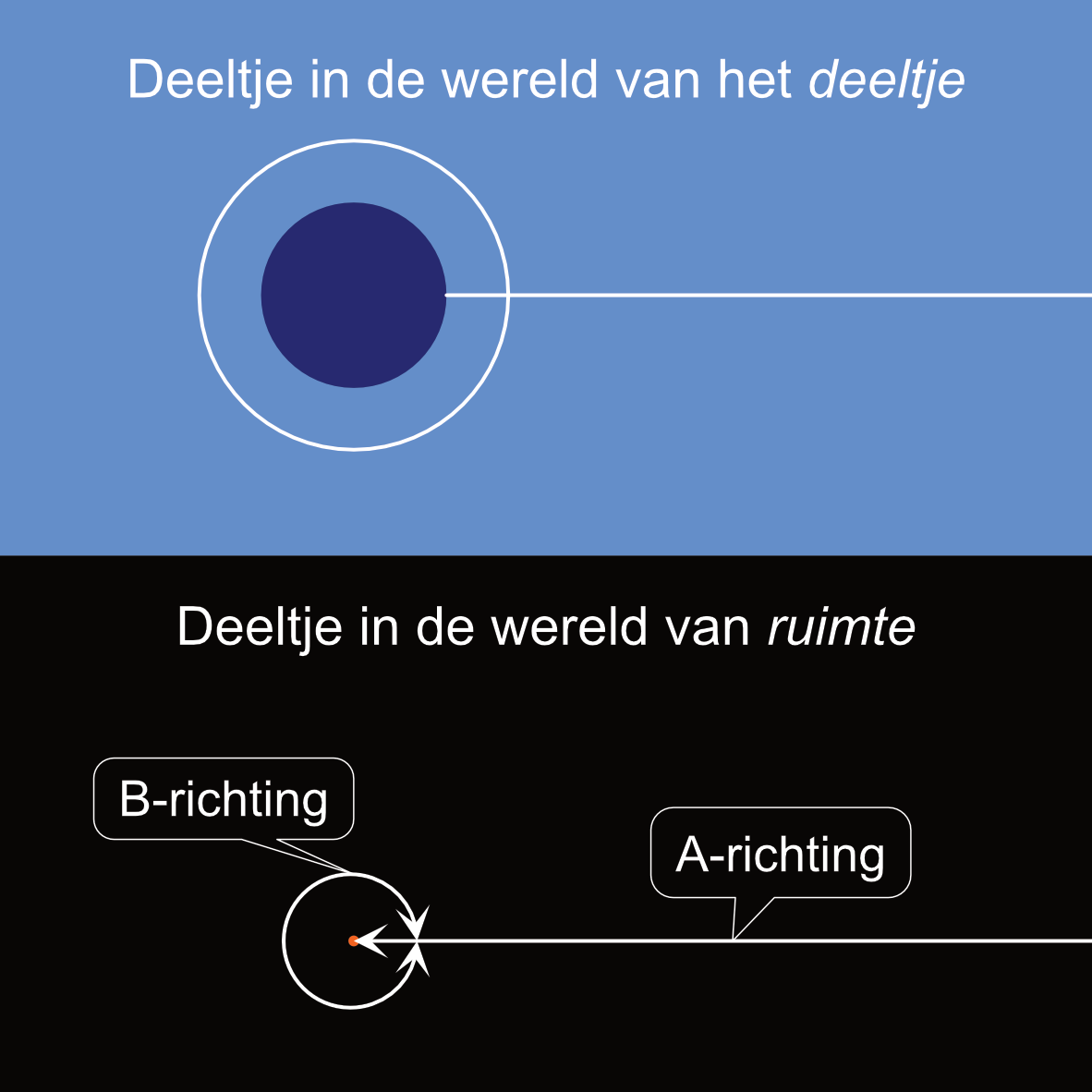
Ik heb in het bovenste gedeelte van deze afbeelding, in de wereld van het deeltje, een witte lijn in de richting van het deeltje en een witte lijn rondom het deeltje getekend. Het zijn denkbeeldige wegen door ruimte. In de wereld van ruimte, in het onderste gedeelte van de afbeelding waar het deeltje geen omvang heeft, laat ik dezelfde wegen zien. De weg naar het deeltje is uitgerekt – ik noem dat de A-richting – maar de weg rondom het deeltje, haaks op de A-richting – ik noem dit de B-richting – is nu flink ingedrukt en lijkt korter maar het is dezelfde weg als in het bovenste gedeelte van de afbeelding.
De A-richting wordt door het deeltje veroorzaakt en door de uitrekking wordt de samendrukking, haaks op de A-richting, in de B-richting veroorzaakt.
In ruimte, op het raakvlak van ruimte en deeltje, is de indrukking in de B-richting bijna oneindig groot. Vanaf het deeltje gezien verloopt de mate van indrukking in de B-richting ook volgens de omgekeerde kwadratenwet (1/afstand²), net als het verloop in de A-richting.
Samendrukking en uitrekking zijn in evenwicht met elkaar en daarom is elk punt in ruimte in evenwicht; het is niet zo dat er door uitrekking ergens een tekort aan ruimte kan ontstaan; ruimte is overal stabiel, alleen de sterkte van de A- en B-richting verschilt per punt in ruimte.
Een deeltje heeft door zijn aanwezigheid invloed op ruimte en die invloed strekt zich uit over de hele ruimte.
Het verloop van de invloed van een deeltje, de omgekeerde kwadratenwet komen we bijvoorbeeld ook tegen in het verloop van zwaartekracht en dat is een aanwijzing dat de invloed van deeltjes de oorzaak van zwaartekracht kan zijn, hoe de A- en B-richting daarin een rol spelen komt later aan de orde.

Belangrijke leerpunten uit deze essay

• Elk deeltje is een entiteit en er zijn er heel veel van.
• Een deeltje=niet-ruimte; en daaruit volgt: ruimte=niet-deeltje.
• Deeltjes zijn de bouwstenen van alle in de werkelijkheid bestaande objecten.
• Deeltjes zijn de enige objecten die in direct contact met ruimte staan.
• Een deeltje in de werkelijkheid kan geen eigenschappen bezitten die tot de wereld van de menselijke ideeën behoren.
• Een deeltje ‘is’ of ‘bezit’ geen afmeting, want afmeting is iets dat wij denken in een synthetisch oordeel over een deeltje in ruimte.
• In de wereld van ruimte is de weg ingekort door het ontbreken van het stukje weg dat door het deeltje is weggenomen.
• De uitrekking naar het deeltje wordt sferisch verdeeld over de hele ruimte. Deze sferische verdeling gaat volgens de zogenaamde omgekeerde kwadratenwet.
• De A-richting (uitrekking) wordt door het deeltje veroorzaakt en door de uitrekking wordt de samendrukking, haaks op de A-richting, in de B-richting (indrukking) veroorzaakt.

Veranderingen vinden alleen in ruimte plaats, maar hoe worden die veranderingen in ruimte doorgegeven, daar gaat de volgende essay in deze reeks over.